A kristály jellemzői
Tartalom
A kristály jellemzői
A kristály (ógörög, krüsztallosz = jég) homogén, diszkontinuális térkitöltésű, anizotróp térrács, aminek külső megnyilvánulása a sík lapokkal határolt mértani test.
- Homogén (egynemű), kémiailag teljesen egységes, legkisebb része is az egész kristállyal azonos összetételű.
- Anizotróp. A kristály tehát egy homogén anizotróp test.
- Rendezett.
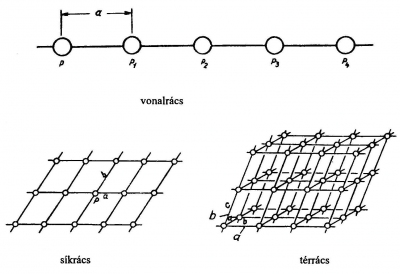
A kristály tehát atomok, ionok, molekulák szabályos periódikus elrendeződése.
Egy, két és három dimenzióra kiterjedő rendezettség
A kristályok sajátságai
Szimmetrián értjük valamilyen motívum szabályszerű ismétlődését. A kristály külső szimmetriája legegyszerűbben az ún. fedési műveletek segítségével ismerhető fel. Morfológiailag három fedési műveletet különböztetünk meg: forgatás, tükrözés, inverzió. Szimmetria elemnek nevezzük azt a mértani elemet, amellyel a fedési műveletet végrehajtjuk
|
Fedési művelet |
Megfelelő szimmetriaelem |
|
forgatás |
gír v. szimmetriatengely |
|
tükrözés |
tükörsík v. szimmetriasík |
|
inverzió |
inverziós pont v. szimmetriaközpont |
Egyszerű szimmetriaelemek
A gír: Olyan szimmetriaelem, amelynek segítségével a kristály egy teljes körforgás alatt önmagával többször fedőhelyzetbe kerül.
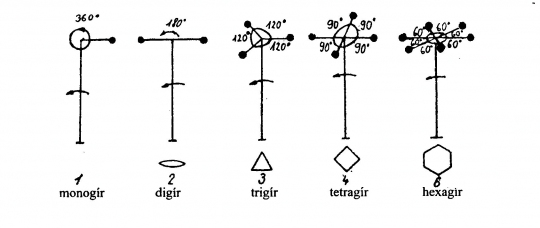
A természetes kristályok lehetséges szimmetriatengelyei (gírjei)
A tükörsík: olyan szimmetriaelem, amely a kristályt két egybevágó tükörképi félre bontja.
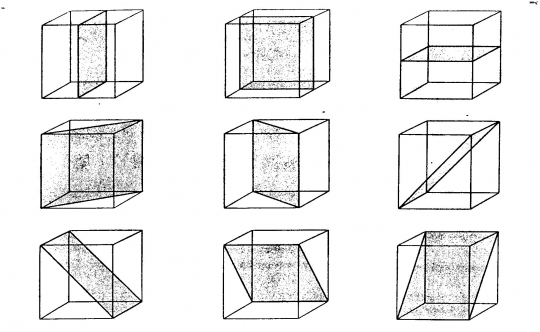
A kocka (hexaéder) 9 szimmetriasíkja
A szimmetria középpont: olyan szimmetriaelem, amelyen áthúzott bármely egyenes azonos kristálytani elemeket köt össze (élt éllel, lapot lappal).
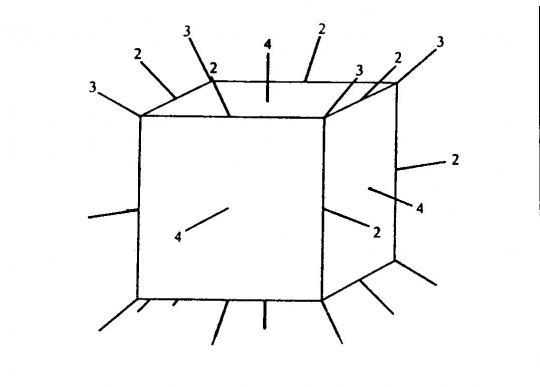
A kocka inverziós pontján átmenő egyenesek.
A számok az egyenessel egybeeső szimmetriatengely értékűségét jelzik
Összetett szimmetriaelemek
Giroid: olyan szimmetriaelem, amely elfordítás közben a kristály eredeti helyzetének a tükörképét is létrehozza.
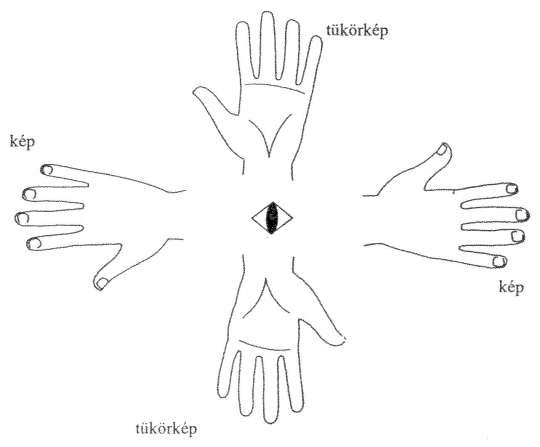
A tetragiorid egyszerű szemléltetése
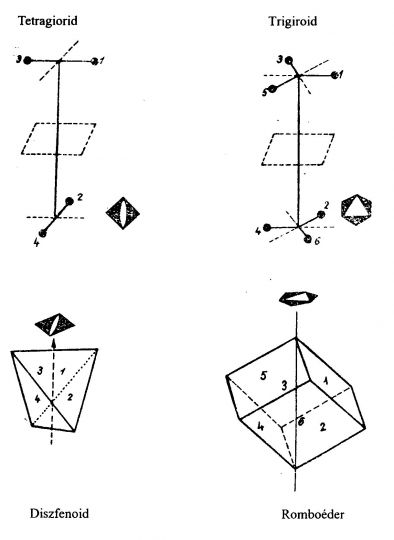
Kristályformák
Az olyan lapok összességét, amely lapok azonos paraméterekkel fejezhetők ki, kristályformának nevezzük. A kristályforma lehet zárt, vagy nyílt. Ha a kristályforma csupa egybevágó lapból áll, egyszerű kristályformáról beszélünk, több egyszerű forma egyidejű fellépése formakombinációt hoz létre. (13/a. ábra). (A segédletben csak a legjellemzőbb formákat tárgyaljuk teljesség igénye nélkül.).
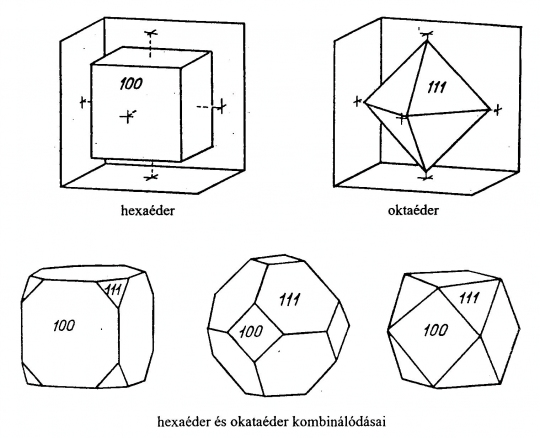
13/a. ábra. a., Egyszerű formák b., Formakombinációk
Nyílt formák:
A nyílt formák lehetnek egy (prizma), vagy két irányban nyíltak (véglap). Nyílt forma a kristályon egymagában nem lehet, csak más formával kombinálódva (13/b. ábra).
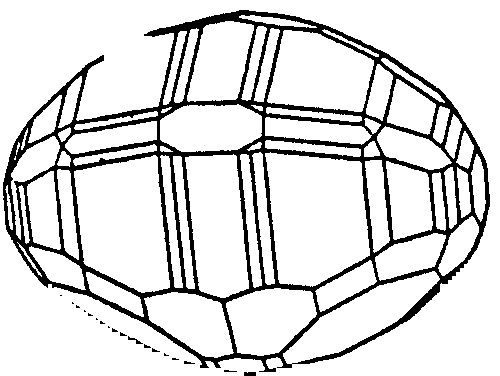
13/b. ábra. Véglapok, prizmák és dipiramisok kombinálódását egy kénkristályon
Véglap vagy (pinakoid (pinax = deszka): 2 lapos kristályforma.
Két párhuzamos lapból áll, amelyek általában inverziós pont szerint tartoznak össze.
Prizma hasáb: azok a formák, melynek lapjai egymással párhuzamos élben metsződnek, és digír, trigír, tetragír, vagy hexagír szerint tartoznak össze.
(A főtengelyes rendszerekben a prizma lapjai a c tengellyel párhuzamosak.)
Piramis: azok a formák, amelyek lapjai a c tengelyhez szimmetrikusan hajolnak.
Zárt forma:
Dipiramis: Poláris szimmetriatengelyre merőlegesen a piramisoknál vízszintes tükörsík lép fel, egy alsó és egy felső piramis dipiramist alkot. (14. ábra)
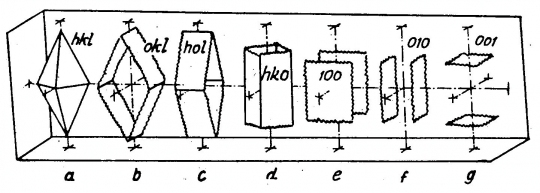
14. ábra. a, dipiramis. b, c, d, prizmák. e, f, g, véglapok
Kristályrendszerek
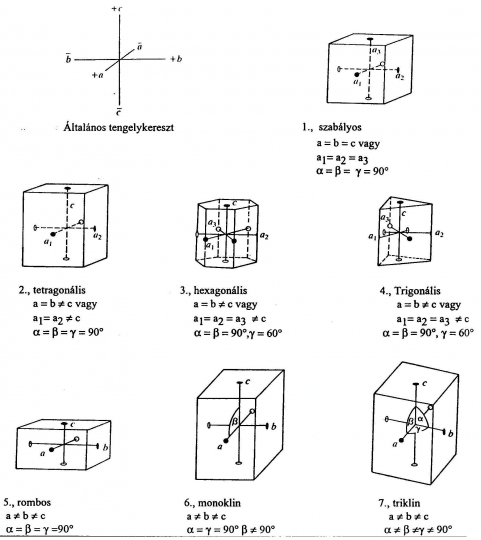
Az összes lehetséges kristályok 7 féle tengelykeresztbe, (7 féle koordinátarendszerbe), illetve 7 kristályrendszerbe sorolhatók:
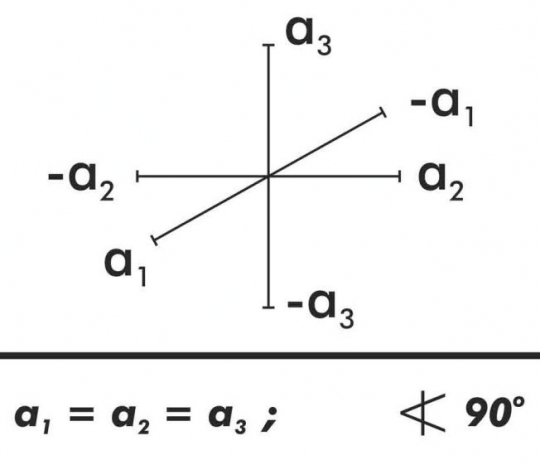
1. Szabályos
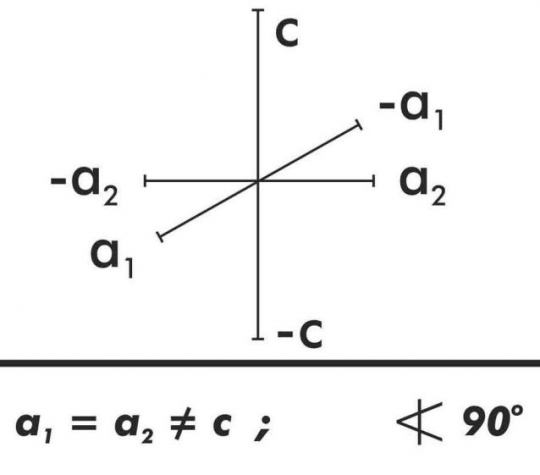
2. Négyzetes
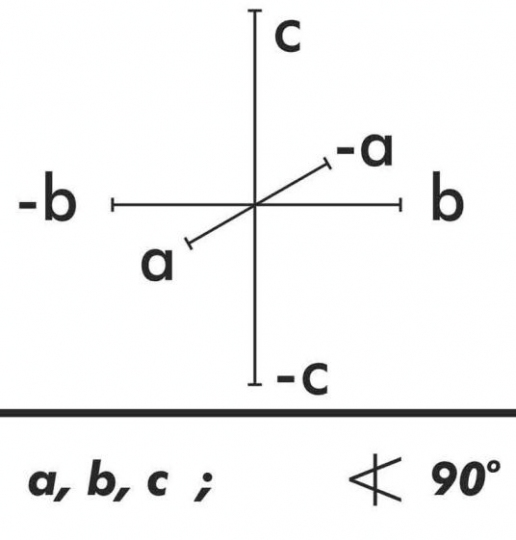
3. Rombos
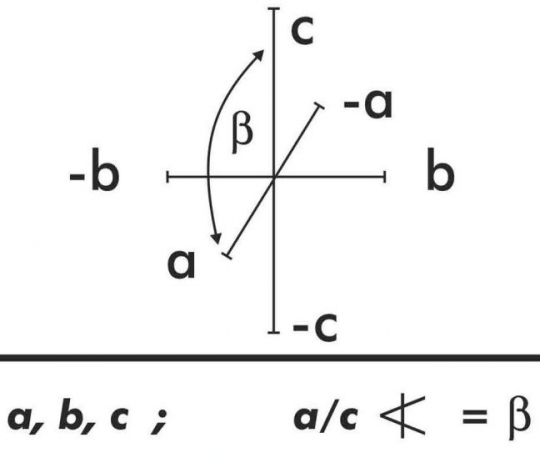
4. Egyhajlású
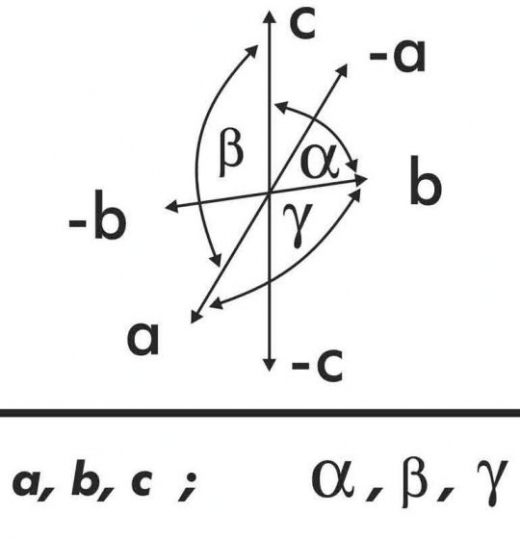
5. Háromhajlású
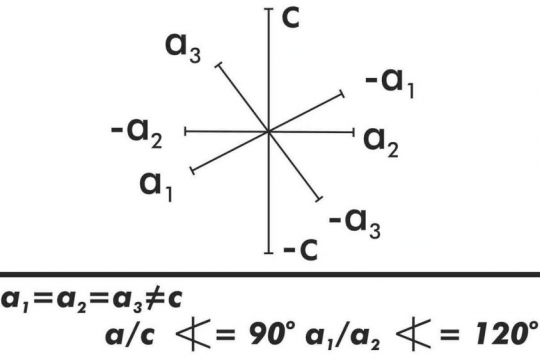
6. Hatszöges
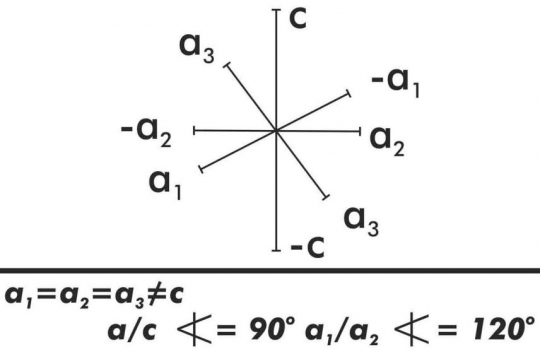
7. Trigonális
Összefoglaló táblázat
Kristálytani tengelyek
A kristálylapok jellemzésére képzeletben térbeli koordinátarendszert létesítünk a kristályban. A koordinátarendszer tengelyei az ún. kristálytani tengelyek a kristály geometriai középpontján mennek keresztül (9. ábra)
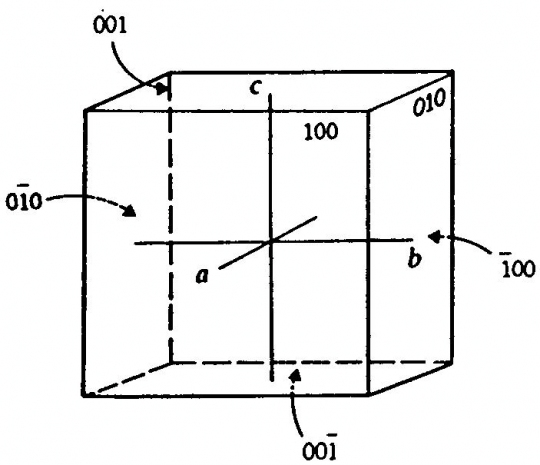
9. ábra. Kristálytani tengelyek a, b, c és a lapok indexei (pl. 001-, -100, stb. l. később)
Paraméter
Azokat a távolságokat, amelyeket az egyes kristálylapok a tengelyekből lemetszenek, paraméternek nevezzük. A kristálylapok jelölésére a paraméterek helyett az ún. Miller féle indexet használjuk. Az indexet a paraméterek reciprok értékei, pl.: (111); (100); (110); stb. Általános esetben a h, k, l, illetve i indexeket alkalmazzuk (9. 10. ábra)
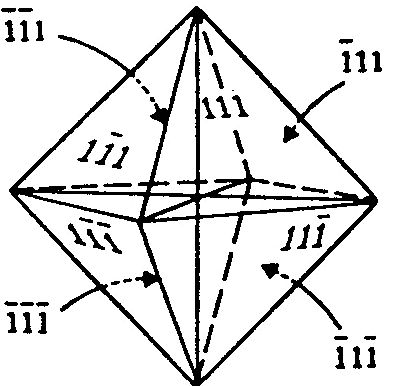
10.ábra. Az oktaéder lapjainak Miller féle indexei
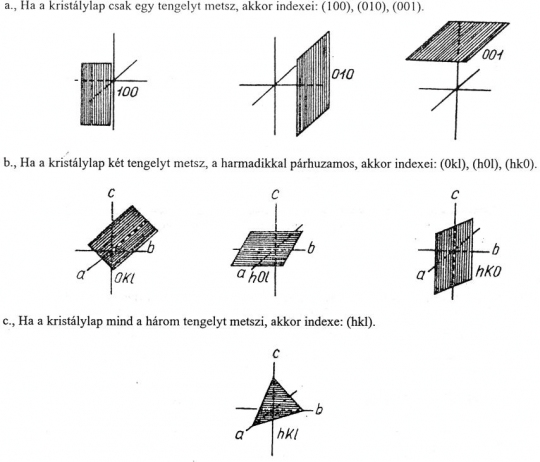
11.ábra. A kristálylapok néhány lehetséges helyzete a tengelykeresztben